Puzzle No. 371 : Kropki Sudoku [Daily League]

Week 14 PDF.

If you’ve not heard yet, LMI has started Beginners’ Puzzle Contests after the success of Beginners’ Sudoku Contests, and the first one is a lovely Classic Masyu Contest!

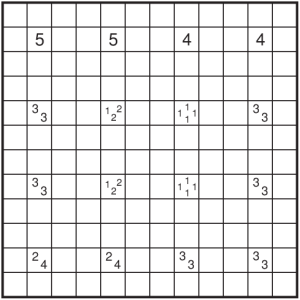
As I said in my last post, I’ve been busy with the Delhi Brain Games event as well as my exams. My exams got over today, and DBG was held successfully on Sunday. So, I’m looking at a relatively not-so-busy schedule ahead (after today). I’ll try to get back to regular posting here again. There’s also gonna be some more puzzle sets I’ll be posting here on some later date. For now, I’m in a hurry to finish things today that have been pending because of my exams + DBG. So, here’s an easy Kropki for the daily league.

Rules – Follow regular Sudoku rules. Additionally, If the absolute difference between two digits in neighbouring cells equals 1, then they’re separated by a white dot. If the digit in a cell is half of the digit in a neighbouring cell, then they’re separated by a black dot.

Enjoy!

P371

Puzzle No. 370 : AntiDiagonal + Fortress Sudoku [Daily League]

Daily League PDF – Week 13.

A little announcement – Around a month or so ago, I was contacted by the people of Sportz Consult, a Sports Management Company that is interested in branching out to Intellectual games. The first such competition, Delhi Brain Games will be held in Delhi this Sunday, and a part of this event is the Solvathon (Instruction booklets available on that link, to those of you who are reading this, are new to puzzles in general, and have registered for the games, these booklets are highly descriptive of what you will be challenged with in the actual events). The Solvathon consists of an hour long Sudoku part and an hour long Puzzle part, and they wanted us (me and Rohan Rao) to provide puzzles for the event. We’ve also provided the material for the Mental Math event.

Since I’ve been busy with this, my exams and many other things, I’ve not been able to give time to posting about this earlier. However, I will say to Indian puzzle enthusiasts in general to watch out for more such events organized by Sportz Consult in the future.

 

Now, back to “business as usual”. Today’s Sudoku is a hybrid. It might be difficult simply based on the hybrid rules coming into play. Both the variants I chose are quite restrictive, but this is one of those where I was particularly adamant to make it work for some reason. In the end it turned out nice enough I think.

Rules – Follow regular Sudoku rules.  Additionally, each of the main diagonals must contain exactly 3 distinct digits. Also, the digits in the shaded cells must be higher than their orthogonal neighbours.

Enjoy!

P370

Puzzle No. 369 : Tapa

Completely random post. I just attempted the Serbian GP on LMI. Didn’t go too well. But the quality of Sudokus is pretty great.

This Tapa isn’t easy, but its not difficult either.

Rules for Tapa.

Enjoy!

P369

Puzzle No. 368 : Outside or Skyscraper Sudoku [Daily League]

This variant is quite tricky in general, but I’ve tried to make at least some of it relatively obvious. Either way, I like the combination, and I like how it turned out.

Rules – Follow regular Sudoku rules. Additionally, the clues outside are at least one of

1. Outside clues – The digit must be placed in one of the first 3 cells in that direction.

2. Skyscraper clues – Taking 1-9 as skyscrapers of increasing heights, 9 being the biggest, the clue shows how many skyscrapers can be seen from that direction. Bigger skyscrapers block smaller ones.

Enjoy!

P368

Puzzle No. 367 : Nanro

Daily League PDF – Week 12.

I just felt like its a day for Nanro. I wanted to use 1×2 regions. A part of this puzzle may be tricky.

Rules – Write numbers in some cells of the grid. All numbers in a region must be the same. The given number in a region denotes how many cells in this region contain a number (all regions must have at least 1 number). Same numbers must not be orthogonally adjacent across region boundaries. Numbered cells must not cover an area of size 2×2 or larger. All numbered cells must form a single orthogonally continuous area..

Enjoy!

P367

Puzzle No. 351 – 366 : Zagreb Open puzzles

I managed to somehow squeeze this set out in one day just before my exams started, right in the middle of the hectic submissions time in college. After that, Vladimir managed to squeeze in some time on that day itself to test these puzzles, so many thanks to him for that.

Rules all placed at the start of the post with the puzzles coming later (Trying a new format for posting, simply because its more convenient for me. The puzzle captions should aid you in knowing which rule is for what puzzle, but the ordering is the same as well, so it shouldn’t be much hassle either way.

Rules –

351 – Akari.

352 – Fillomino.

353 – Graffiti Snake.

354 – Heyawake.

355 – Japanese Sums – Place the digits 1-6 in some of the squares, so that no digit is repeated in any row or column. Sums on the outside indicate the sums of consecutive digits in that row or column, in order. Each sum is seperated by at least one empty square.

356 – LITS.

357 – Nanro – Write numbers in some cells of the diagram. All numbers in a region must be equal. The given number in a region denotes how many cells in this region contain a number (at least one). Same numbers must not be orthogonally adjacent across region boundaries. Numbered cells must not cover an area of size 2×2 or larger. All numbered cells must form a single orthogonally continuous area..

358 – Odd Even Skyscraper – In addition to Skyscraper rules linked to below, all outside clues that are shaded are odd. The rest are even. Range 1-6.

359 – Pentopia.

360 – Regional Yajilin.

361 – Shakashaka.

362 – Skyscrapers. Range 1-6.

363 – Tapa.

364 – Tents – Place a tent ortogonally next to each tree so that no two tents touch eachother, not even diagonally. Numbers on the outside indicate the amount of tents that are in that row or column.

365 – Walls Fillomino – Some region borders are given; i.e. the numbers on both sides must be different.

366 – Yajisan Kazusan.

Enjoy!

P351

P352

P353

P354

P355

P356

P357

P358

P359

P360

P361

P362

P363

P364

P365

P366

Puzzle no. 350 : XV Sudoku [Daily League]

Week 11 PDF.

This one’s on the easy side. I still need work on my converse-rule-sudoku-construction I think.

Rules for Sudoku. Additionally, two neighbouring cells containing digits that add up to 5 are always separated by a V. Two neighbouring cells containing digits that add up to 10 are always separated by an X.

Enjoy!

P350

Puzzle No. 347 – 349 : More UKPA tournament puzzles

It just shows how lost in other things I am, that I actually missed an entire round that had 3 more puzzles of mine. I only realized now while quickly solving through the rounds. The puzzle quality in general is superb. Refer to the previous post for a link to the forum topic where all the puzzles are posted.

Out of these 3, 2 I think are the hardest ones of the set I sent. I guess its appropriate they were used in the team round. The Odd Even Heyawacky requires a lot of thinking of patterns, and the Dotted wall, is just an unfamiliar type with some tricky deductions. The Yajisan Kazusan though, I don’t think is that hard. People who’re used to solving these will find it fine enough until a pause moment near the end, if I remember right. There were 6 more puzzles I sent that’ll be used at a later time. My personal favorites of the set are among those 6.

Anyway, Enjoy! Next post, Tuesday Sudoku.

P347 : Dotted wall – Reading from left to right, top to bottom, every Nth shaded cell is marked by a dot. N is a constant value that needs to be determined by the solver. The shaded cells must form a contiguous wall. No 2×2 group of cells can be entirely shaded. The number at the top of the clue gives the number of shaded cells around it, and the number at the bottom gives the number of dots around it.

P348 : Odd Even Heyawacky – Shade in some cells. No two shaded cells should be adjacent, and all of the unshaded cells should be in one contiguous region. There may never be a horizontal or vertical line of unshaded cells that crosses two thick boundaries. An O in a region means there are an odd number of shaded cells in that region. An E in a region means there are an even number of shaded cells in that region (including zero).

P349 : Yajisan Kazusan – Shade in some cells. Shaded cells cannot be orthogonally adjacent. The remaining white area has to be connected. The clues indicated the number of shaded cells in the direction of the arrow. The clues that are unshaded must be true. Once shaded, a clue is irrelevant.

P347

P348

P349

Puzzle No. 344 – 346 : UKPA Open Tournament puzzles

I’d sent many more puzzles for the UK tournament, but the rounds were put together in a bit of a rush, so a lot of them will be used in future contests, I’m told. Anyway, the 3 that were used, 2 Snake variants, and a LITS are what I’m posting now. Its been a while since the Puzzle Booklets were released on the UK forum so most of you have probably seen these. Still, for the few who haven’t…

On a side note, I’ve been working on a few puzzle sets recently too. While a few of these might/might not make it here, one set in particular will sometime in the next week I think. So, something to look forward to.

Also, try out April Contest by Riad on LMI. Its tough, but there aren’t any time constraints, so one can solve the puzzles at their own pace purely for enjoyment.

Anyway, to the puzzles.

No. 344 – Horse Snake – Blacken some cells so that they form a single continuous path, one cell width (the snake), which head and tail are given. The snake cannot touch itself, even at a point. A clue in a cell corresponds to the number of snake cells (head and tail included) which can be reached in a knight step from this cell. There cannot be any snake segment on a cell containing a clue.

P344

 

 

 

 

 

 

 

No. 345 – Slitherlink Snake – Draw a 1 cell-wide snake of unknown length, not touching itself even diagonally. Its head and tail are marked with circles. The snake cannot go through numbered cells. Numbers show the amount of cells occupied by the snake in the four neighboring cells.

P345

 

 

 

 

 

 

 

No. 346 – LITS – Colour a shape of 4 orthogonally connected squares in each black bordered region so that all coloured squares form a single contiguous area. This area can’t contain any 2×2 coloured squares. Two identical shapes in different regions can’t touch eachother by a side. Rotations and reflections are considered the same shape.

P346

 

Puzzle No. 343 : Disjoint Groups Sudoku [Daily League]

Today’s Sudoku has some difficult spots, because I wanted it to have some difficult spots.

Follow Sudoku Rules. Additionally, all digits have to be in a different position in each 3×3 box.

Enjoy!

P343