IPC Preview – Practice, Solving Tips, Links

Update: Fixed the typo in Pentomino Kakuro. New PDF uploaded. No other change.

Update: There is an erratum published on the IPC site that says the 2×2 restriction applies to Happy Dots too. Since the practice puzzle in the PDF still gives a nice practice for placing the dots and forming regions, and only uses 2×2 regions minimally, it stays the same in the PDF. We’re sorry for the inconvenience. 

If you’re having trouble with some puzzles, seeing/adding to the discussion in the comments might help. (This also serves as a spoiler alert for those who want to work on the puzzles without help)

Right, took a while, but we’re finally there. If you’re still not aware, the Indian Puzzle Championship will be held on 7th July. Here are our (me and Swaroop) best efforts, with the main goal being to try to help the newer participants.

This PDF features –

1. Practice puzzles for B1, B2, C, D, E2, F1, F2, G2, I1, I2, J1, J2, K1, K2, L1, L2, M2.

2. Beginner-level solving tips for all the puzzles in the set.

3. Solutions to all the puzzles in the set.

4.  Links to other practice material, pattern guides, and other technical tips.

Link to PDF – Practice

Enjoy!

Puzzle No. 297 – 312 : Zeka 2013 Puzzle Set

I realize I’m crossing 300 with this without the usual special puzzle, but with Puzzle Marathon coming up, I’m sure everyone will have their fill of special puzzles. I’ll make it up later sometime between 300 and 400. Anyway, this was a 1 hour set at the Croatian competition. I basically started off with trying 1 classic puzzle and one variant of it, but then some pairings are just similar genres. For the variants, I’ll just put the additional rules. The Classic puzzles have links to their rules, and some are fully described here. The difficulties are obviously varied but barring the Pentomino I can’t immediately think of anything particularly difficult. All puzzles tested by Bram De Laat.

Enjoy!

P297 : Bosnian Road.

P297

 

 

 

 

 

 

 

 

 

 

 

P298 : Bosnian Road Odd Even – The clues only give the information that the number in that clue cell is either Odd (O) or Even(E). All the clue substitutions are non-zero.

P298

 

 

 

 

 

 

 

 

 

 

 

P299 : Masyu.

P299

 

 

 

 

 

 

 

 

 

 

 

P300 : Corral Masyu – The cells not visited by the loop must be able to reach the edge of the grid by being orthogonally connected to other such cells.

P300

 

 

 

 

 

 

 

 

 

 

 

P301 : Hashi (Probably the easiest puzzle of the set) – Draw single or double straight lines between the circled numbers. The number in a circle indicates how many lines must end there. The lines must run horizontally or vertically and must not cross or branch off. All circles must be connected to each other; i.e. it must be possible to travel from any circle to any other circle following the lines..

P301

 

 

 

 

 

 

 

 

 

 

 

P302 : Gokigen naname (Known as Slalom in some places like Croco Puzzle) – Draw exactly one diagonal line in each cell of the diagram. A number in some intersections of the grid lines denote how many diagonal lines end in this intersection. The diagonal lines must not form a closed loop.

P302

 

 

 

 

 

 

 

 

 

 

 

P303 : Norinori

P303

 

 

 

 

 

 

 

 

 

 

 

P304 : Trio Cut – Paint some cells to make some triminos so that each trimino will be cut twice by thick lines. Each region bordered by thick lines should have 3 painted cells.

P304

 

 

 

 

 

 

 

 

 

 

 

P305 : Easy As ABC (Range – A-C)

P305

 

 

 

 

 

 

 

 

 

 

 

P306 : Easy as ABC Untouch – Additionally, same letters cannot touch each other even diagonally. Range is A-D.

P306

 

 

 

 

 

 

 

 

 

 

 

P307 : Nurikabe

P307

 

 

 

 

 

 

 

 

 

 

 

P308 : Cipher Nurikabe – The numbers are replaced by letters. All instances of the same letter have same values and different letters have different values. Note that the rule says values, so one letter can stand for a multi-digit number too.

P308

 

 

 

 

 

 

 

 

 

 

 

P309 : Tapa

P309

 

 

 

 

 

 

 

 

 

 

 

P310 : Disjoint Groups Tapa – Additionally, clues in the same box cannot have the same position around them shaded. E.g. 2 clues in the same box cannot both have the cell directly above them shaded.

P310

 

 

 

 

 

 

 

 

 

 

 

P311 : Pentomino – Place the 12 Pentomino pieces into the grid. They can be rotated and reflected. They cannot be placed in black cells. Two pieces cannot touch each other even diagonally. The numbers outside give the number of cells occupied by pentomino pieces in that row or column. Pentominos given at the end of the post.

P311

 

 

 

 

 

 

 

 

 

 

 

P312 : Pentomino Areas – Instead of the numbers outside, the grid is divided into regions, each of which consists of exactly one entire pentomino.

P312

 

 

 

 

 

 

 

 

 

 

 

 

Its as easy as IPC (practice puzzles) (Part 1?)

I’m not numbering these simply because I don’t want to rush to 200 as I’m not ready with an idea for that 😛

These are puzzles that can be used for practice for the Indian Puzzle Championship and you can refer to the Instruction booklet provided on that link for better understanding of the rules with examples.. These are mostly around the difficulty I’ve generally seen at IPC, i.e. , around easy for experienced solvers, somewhere from medium to more for the first time solvers.

I’ve concentrated on types that are not on my blog already. You can see previous posts for Masyu, Slitherlink, Tapa, Graffiti Snake here and here.  I wasted a lot of today making a Liar Slitherlink only to find that I’d made a stupid error right at the start. Thats why only 6 puzzles, I hope to have either a Liar Slitherlink, or some other puzzles ready tomorrow, and Friday. Lets hope I get them working 😉

Anyway, obviously the heading suggests what I’m gonna open with.

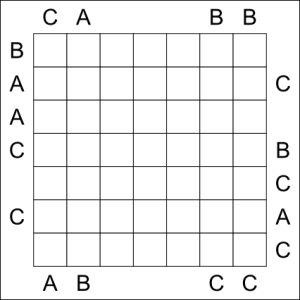
As Easy As IPC

Enter the letters I, P and C, so that each letter appears exactly once in every row and column. Some cells will remain empty in each row and column. The letters outside the grid show the first seen letter from that direction.

 

 

 

 

 

 

 

 

 

Tapa Borders

Paint some empty cells to create a continuous wall. Numbers in a cell indicate the length of painted blocks on its neighboring cells. If a cell has more than one number, there must be at least one white cell between the blocks. No 2×2 squares can contain only painted cells. The borders between some cells may be thick or non existent. A thick border separating two cells means one is painted and one is not. Lack of a border means the 2 cells are either both painted or both white.

 

 

 

 

 

 

 

 

 

 

Battleships 

Locate the indicated fleet in the grid. Each segment of a ship occupies a single cell. Ships can be rotated but cannot be reflected. Ships do not touch each other, even diagonally. Some ship segments, or sea cells without ship segments, are given in the grid. The numbers outside the grid reveal the total number of ship segments in that row or column.

Note : The letters A, B, C may be equal or unequal, the only constraint I’ve added is that their sum equals 4. This is just to introduce first timers to the summing up logic that can be used sometimes in this type.

 

 

 

 

 

 

Snake 

Locate a snake in the grid, whose head and tail are given. The snake does not touch itself even at a point. Numbers outside the grid indicate lengths of snake segments in the corresponding direction.

 

 

 

 

 

 

 

 

 

 

Star Battle 

Place the given number of stars in each row, each column and each region. Stars cannot touch each other, not even diagonally.

 

 

 

 

 

 

 

 

 

 

Colored Star Battle

I’m new to this type myself even as a solver, so the puzzle may leave a lot to be desired. Sorry about that. Although it should be an easy warm up for first timers, I do think the difficulty of the IPC one will be higher given the high points. Anyway,  Place the given number of stars in each row, each column and each region. Similarly colored stars cannot touch each other, not even diagonally. Some stars may be given.